
HOMER Pro 3.16

Type: |
Output Variable |
Units: |
hr |
Symbol: |
Abatt |
The storage bank autonomy is the ratio of the storage bank size to the electric load. HOMER calculates the storage bank autonomy using the following equation:
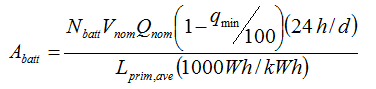
where: |
|
|
|
Nbatt |
= number of batteries in the storage bank |
|
Vnom |
= nominal voltage of a single storage [V] |
|
Qnom |
= nominal capacity of a single storage [Ah] |
|
qmin |
= minimum state of charge of the storage bank [%] |
|
Lprim,ave |
= average primary load [kWh/d] |
